|
|||
Chess and Go Chess and Go are the two greatest examples of a genre of games which are particularly rare: games where all information is known to both players and there is no random element. Thus victory in games of this kind is never accidental. While there are many games of this kind, by far the most important and most famous are the following: (The pen-and-paper games Tic-Tac-Toe and Pig-Pen also fall into this category but they are far less interesting. Chinese Checkers also falls into this category but it's less complicated than any of the ones listed above. And of course, there's always Nim.) Go-moku is a game played with the same pieces as Go but not otherwise related. The goal of the game is to be the first to get five stones in a contiguous row in any direction. Othello is the commercial name of a game first introduced as Reversi, played on the same board as Chess and Checkers use, but with pieces which are white on one side and black on the other. On each move, each player will add one piece to the board and then flip over at least one piece from the opponent's color to their own color. Checkers and Chess are well known in the US. Go (the Japanese word for "battle") is originally a Chinese game, and is heavily played all through the Orient and elsewhere in the world. The best players in the world are now (and have been for centuries) in Japan. The ordering used above is not accidental; they're listed in order of increasing complexity. Chess is inelegant, in my opinion. I've played all five of the games quite extensively, and Chess simply doesn't fit with the others. Three of the others use pieces which are identical, and in Checkers there are only two kinds of pieces and the difference between those is very straightforward (kings can move backward). But Chess? Every piece moves in different ways, and sometimes they interact. Some pieces have a special move their first time. Castling, "en passant", the rules are simply too complicated. You can learn the other games in under five minutes but it's not uncommon for a new player to still be struggling with the rules of Chess for upwards of an hour. I didn't learn about the "en passant" rule until years after I first learned to play. If you didn't know about Go, you might think that complex rules are necessary for a complex and sophisticated game, in as much as the three below Chess on the hierarchy are all much less complex. But Go disproves that, for the rules of Go are extremely simple. Conceptually, if Chess is about political intrigue, then Go is about infantry warfare. A Go-piece should be thought of as a platoon of spearmen. Go is not as popular in the West (though it's quite well known among mathematicians and game aficionados) but you've certainly run into words from it. The company Atari took its name from a word used in Go; it's moderately similar to "Check!" in Chess, and you say it when your most recent move puts an enemy group in imminent peril of death. Go is played on a 19*19 board. By convention the board is a grid of lines, and the pieces are played on the intersections. Players take turn placing pieces on the board, and once a piece is played it never moves unless it is captured and removed from the board. A piece connects to the four spaces next to it vertically and horizontally. Diagonals do not matter in the game. If two pieces of the same color are on contiguous spaces horizontally or vertically, they live and die together. A piece is alive if and only if it is connected to an empty space, or connected to a friendly piece which is connected to an empty space, by any arbitrarily long linking through friendly pieces. One empty space can keep any number of pieces alive. Such empty spaces are called "breathing spaces" (but the conceptual model for me is "farmland", and losing all breathing spaces means that the troop starves). If a group of pieces has its last breathing space filled by the enemy then the group is killed and they are removed from the board. They are kept, as "prisoners", and used at the end during scoring. It is against the rules to fill your own last breathing space and commit suicide. If a piece is played onto the board in such a way that it has no breathing spaces but also removes the last breathing space from an adjacent enemy unit, then the enemy unit loses, dies, is removed from the board and thus creates at least one breathing space for the piece just played. A player may pass and not move at any time when it is his turn to play. Play continues until both players pass. At that point, any "dead" groups are removed from the board as captures (as if they had been killed), and the number of empty spaces each player controls, minus the number of pieces that player lost during play, is his score. If there is dispute about whether a given area is controlled by one player or the other or whether a given unit is "dead", then play continues until the dispute is resolved. In practice this is not an issue. So far the rules are clean and straightforward. The rules to this point do permit an infinite game, and one specific new rule is required to make the game length finite. This is to deal with Ko.
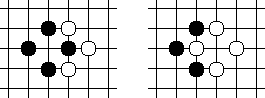
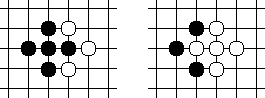
Notice the left board position. The right hand black piece is not connected to the others and can be killed separately. It also only has one breathing space, immediately to its left. If white plays there, then the white piece has no breathing space, but neither does that black piece -- and by the rules of the game the white piece wins and the black piece is killed and removed from the board. This then frees up that space, which becomes a breathing space for White. This transforms the board to the right-hand position. But at that point, Black could simply take the Ko back again, and this could clearly continue until the players died of starvation or old age. So the rule is that when one player takes the Ko, the other player must make his next move somewhere else on the board to permit the Ko to be filled, if desired, by the player that just took it:
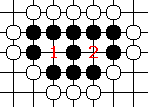
This leads to an interesting thing called a Ko-threat, because sometimes the Ko is needed for one reason or another. Indeed, sometimes the game rides on who wins a particular Ko-battle. A Ko-threat is a move which is meaningless if answered, but devastating if ignored. The goal is to make the opposing player respond to the Ko-threat instead of filling the Ko. If the value of the Ko-threat is greater than the value of the Ko, then the player who just took the Ko will answer the Ko-threat and give the other player a chance to take it back again. Ko's can exchange hands several times before one player runs out of reasonable threats. That's it. That is the complete rules to the game. But there's one derivative of the rules which usually has to be taught explicitly, the definition of "life". Life is two eyes. Suppose that the following black unit exists:
And suppose further that White wants to kill it. Notice that the Black unit has two breathing spaces which are not connected to each other; that's known as two eyes. So White tries to play in empty space "1". White's piece has no breathing spaces, but the Black pieces still have one. By the rules of the game, White's piece dies instantly, and the empty space is restored. In other words, for White to play in "1", "2" must already be filled, and for White to play in "2", "1" also must already be filled. This can't happen, so the Black unit can't be killed. All life comes down to the ability to form two eyes when the unit is under attack, which means to control two breathing spaces which are not connected to each other. It's not usually necessary to actually do so, but you must have the capability. One of your unit is considered "alive" if your opponent acknowledges that he can't prevent you from forming two eyes there. (If he thinks he can, he'll try because doing so would kill the unit, and probably be worth many points.) Equally, one of your units is dead if you acknowledge that you cannot form 2 eyes with it. Now compare that to the rules of Chess, and you can see what I mean about the rules of Chess being so baroque. Every piece in Go is exactly identical, and they don't move. The complexity of the game derives from other things, and it is exceedingly complex. In fact, it is much more complex than Chess. One demonstration of that is the fact that of the five games listed above, Go is the only one for which no computer program can defeat a competent human player (let alone a master). Go-Moku and Othello are relatively easy to program and unbeatable computer programs have existed for them for a long time, even on relatively slow computers. Checkers is far more complex than many people realize, but it appears that this has fallen, too. Extremely good chess programs, capable of defeating any but a Grandmaster, have existed for several years now for standard desktop computers. And recently a specially-built computer from IBM defeated the human world chess champion in a 6-game series under normal tournament rules. Computers have routinely beaten grandmasters at "Blitz-chess", chess played under severe time constraints, but this was the first time that a computer defeated the best human player under normal tournament rules with relaxed time limits. As computers continue to get cheaper and more powerful, it will eventually (within the next 20 years) be possible for a computer affordable by you or me to defeat a grandmaster. But no computerized Go program is even close to "master" status. Ranks in Go use two words Kyu and Dan (pronounced dawn). Players start at 30 Kyu, and as they improve the number drops. (When I was at my best I was about 9 Kyu, American rating scale.) When you reach 1 Kyu and improve again, you become 1 Dan. (This is the same name as is used to denote a first degree black belt in martial arts, incidentally). Then further improvements take you to 2 Dan, 3 Dan etc. I believe that the best players in existence are 9 Dan. Another advantage of Go over Chess is that it is possible to handicap it up to 9 levels without destroying the game. The only way to handicap Chess is for one player to remove a piece before play, but this radically alters the game and changes the dynamics. But in Go, handicaps of between 2 and 9 can exist, and they're implemented by placing black stones (for by convention the less-skilled player always uses the black pieces, which though made of glass are called stones) in certain predefined patterns. If the black player has no handicap, then he moves first (which is, in effect, a one-stone handicap). If the black player has a handicap, then white moves first after the black pieces are placed on the board. The numeric difference between two players indicates the handicap: if a 6 Kyu plays a 10 Kyu then the latter player gets the black pieces with a 4-stone handicap. That is how the ranks are determined: you find a player with a known rank and play him a few times to see what handicap results in an even game. (Once I had an opportunity to play against a 4 Dan. On paper I needed a 14 stone handicap, but 9 was all there was. I got wiped.) When I was at my best I think I could probably have beaten any computer Go program in existence, and at 9 Kyu I was far from "master" status (such as my friend who was 4 Dan). So why is it that a computer program can't play competent Go? To understand that, let's talk first about how the computer programs play the other four games, for the same principle applies to them all. It's done with a brute force tree search, and there are two essential pieces to it. First, there must be a heuristic which permits a board position to be evaluated and assigned a single number score proportional to its desirability. With this heuristic, it must always be possible to compare two board positions to determine which is "better" (or to discover that they're identical). Typically this calculation consumes most of the time. Second, there must be code which can evaluate a board position and determine all the moves which are possible. This is nearly always extremely easy. The program then performs a series of "plies". Each ply consists of looking ahead one move into the future. Taking chess as an example, this is done by taking the current board position and evaluating all the possible moves to determine their point value. The top five (usually) positions (yielding the five highest scores, which means the best positions for "me") are then retained and the rest discarded. On the first ply, one board is evaluated yielding five possible results. For the second ply, each of those five positions is then evaluated to derive all the moves the opponent could make. For each position, all moves are evaluated and the top five (the five with the lowest scores, meaning the ones which are best for "him") are retained. This yields 25 boards at the end of two plies. For the third ply, each of those 25 boards is again evaluated looking for the top five moves, yielding 125 boards. On the fourth ply the result is 625 boards. And so on. As you can see, the compute load explodes the further out you look. To play a competent game you need to look out at least 6 plies. Each board may yield anything up to 30 possible moves to evaluate in order to pick the 5 best. To defeat a Kasparov you need a lot more than 6. To augment this, the program is usually programmed with a big "book", a database of games from history (mainly openings) with attached calculated values for those board positions. While the computer program is "playing in its book" it isn't necessary for it to do the brute force evaluation described above, and it is capable of working quite rapidly (a fraction of a second per move, with the work consisting of hashing the board position and accessing a database). Kasparov's idea in playing against Deep Blue (the program which beat him) was to try to use strange moves to try to break it out of its book as fast as possible. Unfortunately, this backfired on him because it turned out that Deep Blue had a better "book" than he did (and thus in a couple of cases the computer was playing from its database while Kasparov was using evaluation) and in any case it turned out that Deep Blue was very good and very fast at brute force evaluation. But to accomplish this IBM had built the fastest parallel computer in existence, running code which had been fine tuned. One of the difficult parts is creating the position-evaluation heuristic, but there's been a lot of research into this on Chess and those algorithms are pretty well understood now. Look far enough out and the problem is finite but too big to be solved in the life of the universe. No computer (or human either) will ever look 20 plies out. If the computer can evaluate enough, though, and if it doesn't have any algorithmic weaknesses, then it will play a uniformly strong game throughout (where humans sometimes make questionable plays) and will be extremely difficult to beat. While the team at IBM were developing Deep Blue, they had the assistance of one of the top ten Chess players in the world, who would come and play against it. If he won, they would then analyze the game and see where the program had screwed up. Often this involved fine tuning the position-evaluation heuristic, for instance, to change the relative values of various things e.g. how much is a "passed pawn" worth on the sixth rank compared to the ability to place the enemy king in check or the potential to castle on Queen's side? That is also how the other computer game players work, only for them the evaluation is faster which means that for the same compute time it's possible to look out more plies. It's a truism that the more plies a program can calculate, the better it will play. It's possible to create an unbeatable Othello program on even a moderately powerful computer. (There are refinements to this, like tree-trimming algorithms, which drastically enhance the efficiency, but they only somewhat ameliorate the exponential explosion of the compute problem.) But this approach fails on Go because it's overwhelmed by numbers. First, as an experience programmer and an experienced Go player, I wouldn't have any idea how to write a comprehensive board-evaluation algorithm. Some things are easy to evaluate (primarily tactical), but some strategic issues, which are enormously important, are intractable. A game can be lost in the first 16 moves and between competent players those moves will be exclusively strategic. (And the devil is in the details. The value of a play can change dramatically if it is one space off.) But even if a reasonable evaluation algorithm could be found, it wouldn't help. In Chess there are rarely more than 30 possible moves on the board, most of which are foolish. So you can do quite nicely with retaining five positions per ply for each previous board. And if you can look out 8 plies, then your program will play a very powerful game. However, in Go the board starts with 361 empty spaces and all of them have to be evaluated. In the mid-game there can be 200 moves. And of them, usually fifty (and sometimes as many as a hundred) may potentially be reasonable. Worst of all, when I was good I would quite often look out as much as 20 moves before deciding what I wanted to do, and I have no doubt at all that a Dan-level player looks further out than that sometimes. So instead of looking out 10 plies with a branching level of 5 requiring evaluating 510 positions at the furthest level of the ply, nearly 10 million, which is nowhere near enough to defeat a Kasparov, it would be necessary to retain 50 positions on each ply and look out at least 20 plies yielding a calculation load of 5020 at the horizon, approximately 1034 boards at the last ply. Even if your computer was fast enough to evaluate that many positions, there's not enough computer memory in existence to store them all (approximately 1036 bytes), nor can any computer in existence access that much memory. Worse, the value of some moves can't be determined without look out as much as a hundred plies. This is a difference in degree sufficient to become a difference in kind. No computer available now or which will become available within the foreseeable future is capable of dealing with numbers like these. All the computers in the world working collectively couldn't do that, and 10 plies isn't very much for Go; it wouldn't be enough to defeat a 9 Don. Not even close. Branching 100 times and looking 100 plies out requires evaluating 10200 positions at the horizon, a number which is far larger than the number of elementary particles in the Universe -- which means that it is theoretically impossible to do this because it can't be stored. So the approach which works for the other four games can't work for Go. To make a competent computer Go player, a different concept than brute-force tree search will be needed. Right now no-one has any idea what that might be. But we know it can be done, because humans do it. So how do humans do it? As a general rule, for any of these games, humans have an extremely efficient tree-trimming algorithm because they have an extremely sophisticated board position evaluation algorithm. A human doesn't search a branching tree; rarely does a human have to follow more than ten or twenty branches even when looking out 8 or 10 moves. Though I can play the game of Go, I'm not sure I can describe how I evaluate a board position. I know that I use "visual thinking" instead of logical-verbal thinking, and that when I'm looking ahead I store the position as a picture in my head. Some of my strategic moves are based on a kind of conceptual "field", with each of my pieces generating positive fields and my enemies pieces generating negative fields -- at least strategically. It's difficult to explain. The experience of playing Go is not dissimilar to the experience of playing chess, in fact, except for the details of the game. There are patterns you learn to recognize (e.g. "the ladder", "the monkey jump", "the snapback" -- I used to play against a guy who was a sucker for snapbacks and never seemed to spot them) but they come up less than you might think (especially sucker-plays like the monkey-jump which are easily prevented). Also, while openings in Chess are extremely well understood and even when Grandmasters play they rarely deviate from known patterns before the 9th or 10th move of the game, the equivalent in Go ("corners") are only guidelines and you tend to leave established patterns quite rapidly. Also, each corner is fought separately, so in Go there are four openings instead of only one, with the outcome of the game caused by the interaction between those four and the other moves played along the sides. There are also rather odd stratagems. When playing against someone less skilled than I am, sometimes I'll make moves simply to make the position complex even though I don't necessarily know the outcome. What I'm relying on is that I'll see my way through the tangle and already have the battle won before my less skilled opponent has figured out what is going on. Thus there will be a period in which I'm playing both strategically and tactically (because I see the end) and my opponent is only playing tactically (because he doesn't). All of the complexity of Go derives from the huge space in which it is played. The difference between a 64-location board and a 361-location board is dramatic. Within that space, (all of which gets used before the game is over) the simple rules merely facilitate complex play, rather than forcing it by being arcane (as is the case in Chess). Go has some of the attraction of The Game of Life, where simple rules can yield extremely complex results, simply through scaling. And that is why I love it -- from simplicity comes elegance; from size comes complexity. "A minute to learn, a lifetime to master" applies to any of these games (except Chess, which takes too long to learn) but more to Go than any other. No other game known to me has such simple rules and such complex play. This page has been viewed 3489 times since 20010726. |
|||